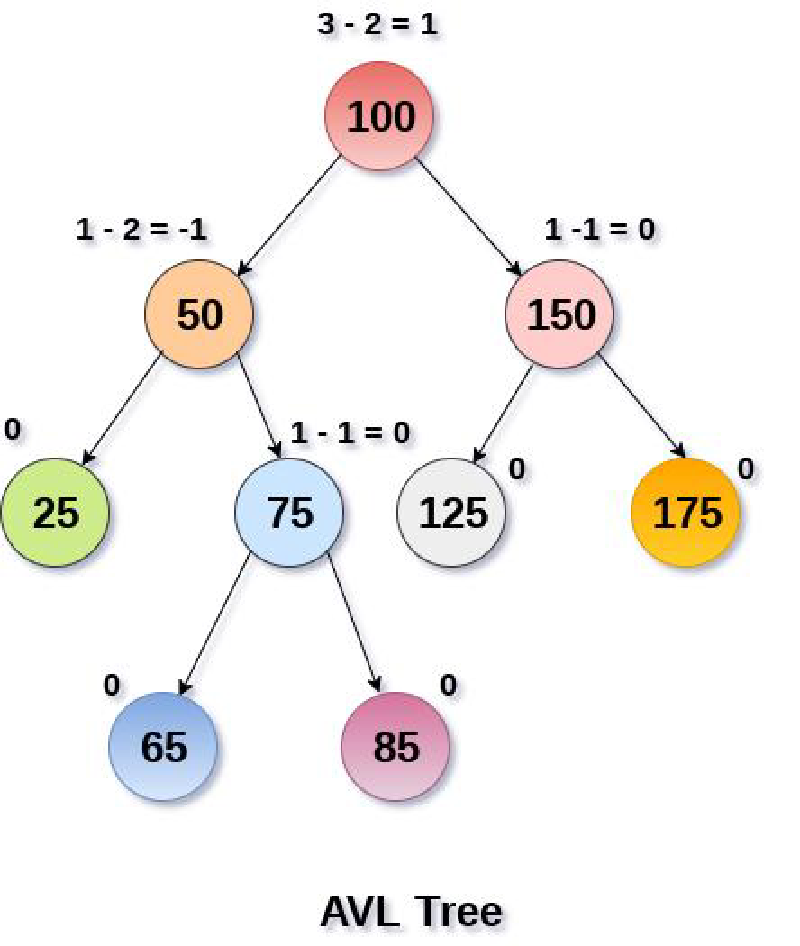
平衡二叉树
数据结构定义
// 定义树的节点
template<class T>
class AvrTreeNode
{
public:
AvrTreeNode(){};
AvrTreeNode(T data)
{
this->data = data;
left = 0;
right = 0;
hight = -1;
}
~AvrTreeNode(){};
T data; // 存储的数据
AvrTreeNode *left; // 左子树
AvrTreeNode *right; // 右子树
int hight; // 高度
};
// 定义树
template<class T>
class AvrTree
{
private:
AvrTreeNode<T> *root; // 定义根节点
// 插入节点
void inseartNode(AvrTreeNode<T>*& node, const T data);
void deleteNodeAll(AvrTreeNode<T> *node); // 删除所有节点
// 显示节点
void DLR(AvrTreeNode<T> *node);
void LDR(AvrTreeNode<T> *node);
void LRD(AvrTreeNode<T> *node);
// 删除*&代表指针引用
bool deleteNode(AvrTreeNode<T>*& node, const T data);
// void deleteNodeByMerge(AvrTreeNode<T>*& node); // 合并删除
// void deleteNodeByCopy(AvrTreeNode<T>*& node); // 复制删除
// 单右旋
void LL(AvrTreeNode<T> *&node);
// 单左旋
void RR(AvrTreeNode<T> *&node);
// 左右旋
void RLR(AvrTreeNode<T> *&node);
// 右左旋
void LRR(AvrTreeNode<T> *&node);
// 求高度的最大值
int maxHight(int h1, int h2)
{
return h1>h2 ? h1:h2;
}
// 得到树的高度
int getTreeHight(AvrTreeNode<T> *node)
{
if(!node)
{
return -1;
}
return node->hight;
}
public:
AvrTree(/* args */)
{
root = 0;
}
~AvrTree();
// 清空树
void clear();
// 是否为空树
bool isEmpty()
{
return root == 0;
}
// 插入数据
void inseartData(const T data);
// 深度优先遍历树
// 前序遍历(DLR 根->左->右)
void showNodeByDLR();
// 中序遍历(LDR 左->根->右)
void showNodeByLDR();
// 后序遍历(LRD 左->右->根)
void showNodeByLRD();
// 删除节点的数据
bool remove(const T data);
// LVR查找树
bool LVRSearchData(const T data);
};
数据操作
数据的插入
// 数据的插入
template<class T>
void AvrTree<T> ::inseartNode(AvrTreeNode<T> *& node, const T data)
{
// 如果节点为空
if(node == 0)
{
node = new AvrTreeNode<T>(data);
return;
}
// 插入在左子树
if(data < node->data)
{
inseartNode(node->left, data);
// 树不平衡时
if(getTreeHight(node->left) - getTreeHight(node->right) > 1)
{
// 当值比左节点的值小时,则进行单右旋
if(data < node->left->data)
{
LL(node);
}
// 否则进行左右旋
else
{
RLR(node);
}
}
}
// 插入在右子树
else
{
inseartNode(node->right, data);
// 树不平衡时
if(getTreeHight(node->right) - getTreeHight(node->left) > 1)
{
// 当值比右节点的值大时,则进行单左旋
if(data >= node->right->data)
{
RR(node);
}
// 否则进行右左旋
else
{
LRR(node);
}
}
}
// 重新计算节点的高度,节点的深度+1
node->hight = maxHight(getTreeHight(node->left), getTreeHight(node->right)) + 1;
}
template<class T>
void AvrTree<T> ::inseartData(const T data)
{
// 如果为空树
if(isEmpty())
{
root = new AvrTreeNode<T>(data);
root->hight = 0;
return;
}
inseartNode(root, data);
}
数据的删除
// 数据的删除
template<class T>
void AvrTree<T> ::deleteNodeAll(AvrTreeNode<T> *node)
{
if(node == 0)
{
return;
}
// 删除左节点
deleteNodeAll(node->left);
// 删除右节点
deleteNodeAll(node->right);
// 释放节点
delete node;
}
template<class T>
void AvrTree<T> ::clear()
{
// 如果为空树,直接返回
if(root == 0)
{
return;
}
deleteNodeAll(root);
}
template<class T>
bool AvrTree<T> ::deleteNode(AvrTreeNode<T> *& node, const T data)
{
// 如果节点为空,直接返回,表示未找到数据
if(!node)
{
cout << "no find:" << data << endl;
return false;
}
// 找到数据节点
if(data == node->data)
{
AvrTreeNode<T> *temp = node;
// 只有右节点
if(!node->left)
{
node = node->right;
}
// 只有左节点
else if(!node->right)
{
node = node->left;
}
else
{
// 采用合并的方式进行删除节点
temp = node->left;
// 找到左子树的做大值
while (temp->right)
{
temp = temp->right;
}
temp->right = node->right;
temp = node;
node = node->left;
// 是否对树进行调整
if(getTreeHight(node->left)-getTreeHight(node->right) > 1)
{
// 值比最大值大或者等于,就采用单左旋
if(data >= node->right->data)
{
RR(node);
}
//采用先右旋在左旋
else
{
LRR(node);
}
}
}
// 删除节点,返回
delete temp;
if(node)
{
node->hight = maxHight(getTreeHight(node->right), getTreeHight(node->right)) + 1;
}
return true;
}
// 在左子树查找
else if(data < node->data)
{
deleteNode(node->left, data);
// 是否对树进行调整
if(getTreeHight(node->left)-getTreeHight(node->right) > 1)
{
// 如果值比左子树小,就采用单右旋,
if(data < node->left->data)
{
LL(node);
}
// 采用先左旋在右旋
else
{
RLR(node);
}
}
}
// 在右子树查找
else
{
deleteNode(node->right, data);
// 是否要对树进行调整
if(getTreeHight(node->right) - getTreeHight(node->left) > 1)
{
// 值比最大值大或者等于,就采用单左旋
if(data >= node->right->data)
{
RR(node);
}
// 采用先右旋在左旋
else
{
LRR(node);
}
}
}
// 对节点的深度进行调整
node->hight = maxHight(getTreeHight(node->right), getTreeHight(node->right)) + 1;
}
template<class T>
bool AvrTree<T> ::remove(const T data)
{
// 如果为空树
if(isEmpty())
{
cout << "this tree is empty" << endl;
return false;
}
return deleteNode(root, data);
}
数据的查询
// 数据的查询
template<class T>
void AvrTree<T> ::DLR(AvrTreeNode<T> *node)
{
if(!node)
{
return;
}
// 前序遍历(DLR)(根->左->右)
cout << node->data << "->";
DLR(node->left);
DLR(node->right);
}
template<class T>
void AvrTree<T> ::LDR(AvrTreeNode<T> *node)
{
if(!node)
{
return;
}
// 中序遍历(LDR)(左->根->右)
LDR(node->left);
cout << node->data << "->";
LDR(node->right);
}
template<class T>
void AvrTree<T> ::LRD(AvrTreeNode<T> *node)
{
if(!node)
{
return;
}
// 后序遍历(LRD)(左->右->根)
LRD(node->left);
LRD(node->right);
cout << node->data << "->";
}
template<class T>
void AvrTree<T> ::showNodeByDLR()
{
if(isEmpty())
{
cout << "this tree is empty" << endl;
return;
}
// 遍历树
AvrTreeNode<T> *node = root;
cout << "DLR: ";
DLR(node);
cout << endl;
}
template<class T>
void AvrTree<T> ::showNodeByLDR()
{
if(isEmpty())
{
cout << "this tree is empty" << endl;
return;
}
// 遍历树
AvrTreeNode<T> *node = root;
cout << "LDR: ";
LDR(node);
cout << endl;
}
template<class T>
void AvrTree<T> ::showNodeByLRD()
{
if(isEmpty())
{
cout << "this tree is empty" << endl;
return;
}
// 遍历树
AvrTreeNode<T> *node = root;
cout << "LRD: ";
LRD(node);
cout << endl;
}
template<class T>
bool AvrTree<T> ::LVRSearchData(const T data)
{
// 如果树为空就直接返回
if(isEmpty())
{
return false;
}
AvrTreeNode<T> *node = root;
while (node)
{
if(data == node->data)
{
return true;
}
else if(data < node->data)
{
node = node->left;
}
else
{
node = node->right;
}
}
return false;
}
树的旋转
// 节点的旋转
template<class T>
void AvrTree<T> ::LL(AvrTreeNode<T> *& node)
{
// 临时节点为节点的左节点
AvrTreeNode<T> *temp = node->left;
// 节点的左节点指向临时节点的右节点
node->left = temp->right;
// 临时节点的右节点指向节点(将临时节点的设置为根)
temp->right = node;
// 重新获得树的高度
temp->hight = maxHight(getTreeHight(temp->left), getTreeHight(temp->right)) + 1;
node->hight = maxHight(getTreeHight(node->left), getTreeHight(node->right)) + 1;
// 经node 重新指向temp, 即将temp设置为根节点,防止树的断
node = temp;
}
template<class T>
void AvrTree<T> ::RR(AvrTreeNode<T> *& node)
{
// 临时节点为节点的右节点
AvrTreeNode<T> *temp = node->right;
// 节点的右节点指向临时节点的节点
node->right = temp->left;
// 临时节点的左节点指向节点
temp->left = node;
// 重新计算树的高度
temp->hight = maxHight(getTreeHight(temp->left), getTreeHight(temp->right)) + 1;
node->hight = maxHight(getTreeHight(node->left), getTreeHight(node->right)) + 1;
// 经node 重新指向temp, 即将temp设置为根节点,防止树的断
node = temp;
}
template<class T>
void AvrTree<T> ::RLR(AvrTreeNode<T> *& node)
{
// 先进行左旋
RR(node->left);
// 在进行右旋
LL(node);
}
template<class T>
void AvrTree<T> ::LRR(AvrTreeNode<T> *& node)
{
// 先进行右旋
LL(node->right);
// 在进行左旋
RR(node);
}
测试
int main(int argc, char const *argv[])
{
AvrTree<int> avr;
avr.inseartData(12);
avr.inseartData(42);
avr.inseartData(93);
avr.inseartData(4);
avr.inseartData(15);
avr.inseartData(66);
avr.inseartData(97);
avr.showNodeByDLR();
cout << "***********************************" << endl;
avr.showNodeByLDR();
cout << "***********************************" << endl;
avr.showNodeByLRD();
cout << "***********************************" << endl;
bool ok = avr.remove(42);
cout << "remove is:" << ok << endl;
avr.showNodeByDLR();
cout << "***********************************" << endl;
avr.showNodeByLDR();
cout << "***********************************" << endl;
avr.showNodeByLRD();
cout << "***********************************" << endl;
bool is = avr.remove(12);
cout << "remove is:" << is << endl;
avr.showNodeByDLR();
cout << "***********************************" << endl;
avr.showNodeByLDR();
cout << "***********************************" << endl;
avr.showNodeByLRD();
cout << "***********************************" << endl;
bool is1 = avr.remove(661);
cout << "remove1 is:" << is1 << endl;
avr.showNodeByDLR();
cout << "***********************************" << endl;
avr.showNodeByLDR();
cout << "***********************************" << endl;
avr.showNodeByLRD();
cout << "***********************************" << endl;
bool ok_ = avr.LVRSearchData(66);
cout << "SearchData is:" << ok_ << endl;
system("pause");
return 0;
}
源码