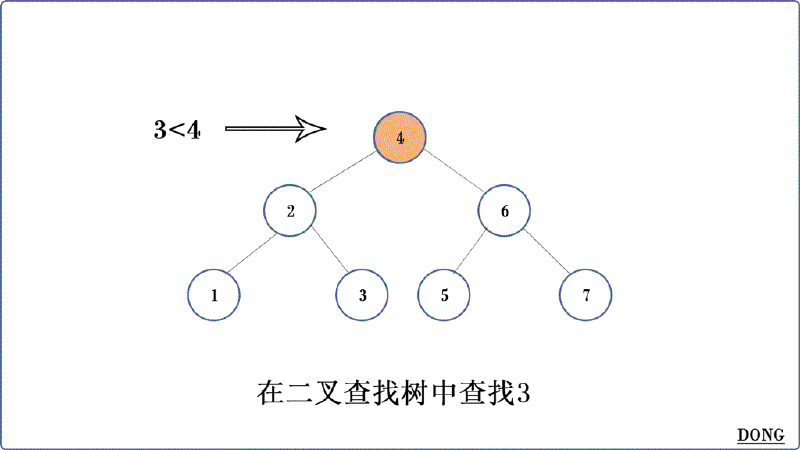
二叉查找树
数据结构定义
// 节点的定义
template<class T>
class BinarySearchTreeNode
{
public:
BinarySearchTreeNode()
{
left = 0;
right = 0;
}
BinarySearchTreeNode(T data)
{
this->data = data;
left = 0;
right = 0;
}
~BinarySearchTreeNode(){};
T data; // 保存的节点的数据
BinarySearchTreeNode *left; // 指向左节点
BinarySearchTreeNode *right; // 指向右节点
};
// 树的定义
template<class T>
class BinarySearchTree
{
private:
BinarySearchTreeNode<T> *root; // 定义头节点
int treeNodeNum; // 树的节点数
void deleteNodeAll(BinarySearchTreeNode<T> *node); // 删除所有节点
// 显示节点
void DLR(BinarySearchTreeNode<T> *node);
void LDR(BinarySearchTreeNode<T> *node);
void LRD(BinarySearchTreeNode<T> *node);
// 删除*&代表指针引用
void deleteNodeByMerge(BinarySearchTreeNode<T>*& node); // 合并删除
void deleteNodeByCopy(BinarySearchTreeNode<T>*& node); // 复制删除
public:
BinarySearchTree()
{
root = 0;
treeNodeNum = 0;
};
~BinarySearchTree();
// 清空树
void clear();
// 节点的个数
int Nodes()
{
return treeNodeNum;
}
// 是否为空树
bool isEmpty()
{
return root == 0;
}
// 插入数据
void inseartNode(const T data);
// 深度优先遍历树
// 前序遍历(DLR 根->左->右)
void showNodeByDLR();
// 中序遍历(LDR 左->根->右)
void showNodeByLDR();
// 后序遍历(LRD 左->右->根)
void showNodeByLRD();
// 删除节点的数据
// 合并删除
bool removeNodeMerge(const T data);
// 复制删除
bool removeNodeCopy(const T data);
// 查找数据
bool SearchData(const T data);
};
数据操作
数据的插入
template<class T>
void BinarySearchTree<T> ::inseartNode(const T data)
{
BinarySearchTreeNode<T> *new_node = new BinarySearchTreeNode<T>(data);
// 如果为空树
if(isEmpty())
{
root = new_node; // 新建节点设置为root 节点
treeNodeNum ++; // 树的节点数+1
return;
}
BinarySearchTreeNode<T> *node = root;
// 遍历树, 找到插入的节点的位置
while (node != 0)
{
// 当节点的值大于插入的值时,就插入到左子数
if(node->data > data)
{
// 左节点为nill, 将新节点赋值给节点的左节点
if(node->left == NULL)
{
node->left = new_node;
break; // 推出循环
}
else
{
node = node->left;
continue; // 继续查找下一个节点
}
}
else
{
// 如果右节点为nill, 右节点->新节点
if(node->right == NULL)
{
node->right = new_node;
break;
}
else
{
node = node->right;
continue;
}
}
}
treeNodeNum ++; // 数的节点数+1
}
数据的删除
// 采用递归的方式删除节点
template<class T>
void BinarySearchTree<T> ::deleteNodeAll(BinarySearchTreeNode<T> *node)
{
// 如果的空树就结束递归
if(node == 0)
{
return;
}
deleteNodeAll(node->left);
deleteNodeAll(node->right);
cout << node->data << endl;
delete node; // 释放资源
}
template<class T>
void BinarySearchTree<T> ::clear()
{
deleteNodeAll(root); // 清空所有节点
treeNodeNum = 0; // 树的节点数为0
}
/*
合并删除法:
从删除的节点的两棵子树合并未一棵树,然后将这颗树连接到删除节点的父节点
具体操作:左子树的最大值左作为有子树的父节点,左子树的根节点作为这棵树的根节点
或右子树的最小值作为左子树的父节点,右子树的根节点作为这棵树的根节点
*/
template<class T>
void BinarySearchTree<T> ::deleteNodeByMerge(BinarySearchTreeNode<T>*& node)
{
// 左子树作为root作为树的root
/*
BinarySearchTreeNode<T> *temp = node;
if(node != 0)
{
// 如果节点的左节点为空
if(!node->left)
{
node = node->right; //直接指向node的右节点
}
// 如果右子节点为空
else if(!node->right)
{
node = node->left; // 直接指向node的左节点
}
else{
temp = node->left; // temp 为node的左节点
// 找出左节点中的最大值
while (temp->right)
{
temp = temp->right;
}
temp->right = node->right; // 左子树的最大值指向右节点
temp = node;
node = node->left; // 左子树作为两颗树的头节点
}
delete temp;
} */
// 右子树的root作为树的root
BinarySearchTreeNode<T> *temp = node;
if(node)
{
if(!node->left)
{
node = node->right;
}
else if(!node->right)
{
node = node->left;
}
else
{
temp = node->right;
while (temp->left)
{
temp = temp ->left;
}
temp ->left = node->left;
temp = node;
node = node->right;
}
delete temp;
}
}
/*
复制删除法:
将被删除节点的左子树的最大值或者右子树的最小值复制给被删除的节点的数值,
然后删除左子树的最大值的节点或者右子树的最小值的节点
*/
template<class T>
void BinarySearchTree<T> ::deleteNodeByCopy(BinarySearchTreeNode<T>*& node)
{
// 复制右子树的最小值
/*
BinarySearchTreeNode<T> *prev = 0; // 复制节点(右子树最小值被删节点)的前驱节点
BinarySearchTreeNode<T> *temp = node;
if(node)
{
if(!node->left)
{
node = node->right;
}
else if(!node->right)
{
node = node->left;
}
else
{
temp = node->right;
// 找到右子树的最小值
while (temp->left)
{
prev = temp;
temp = temp->left;
}
node->data = temp->data; // 将右子树的最小值复制给被删节点
// 当右子树的首节点没有左节点时
if(prev == node)
{
node->right = temp->right; // 直接指向被删节点的右节点
}
else
{
prev->left = temp->right; // 先驱节点的左节点指向删除节点的右节点
}
}
delete temp;
}*/
// 复制左子树的最大值
BinarySearchTreeNode<T> *prev = 0; // 复制节点(右子树最小值被删节点)的前驱节点
BinarySearchTreeNode<T> *temp = node;
if(node)
{
if(!node->left)
{
node = node->right;
}
else if(!node->right)
{
node = node->left;
}
else
{
temp = node->left;
// 找到左子树的最大值
while (temp->right)
{
prev = temp;
temp = temp->right;
}
node->data = temp->data; // 将左子树的最大值复制给被删节点
// 当左子树的首节点没有右节点时
if(prev == node)
{
node->left = temp->left; // 直接指向被删节点的左节点
}
else
{
prev->right = temp->left; // 先驱节点的右节点指向删除节点的左节点
}
}
delete temp;
}
}
// 合并删除
template<class T>
bool BinarySearchTree<T> ::removeNodeMerge(const T data)
{
if(isEmpty())
{
cout << "the tree is empty" << endl;
return false;
}
BinarySearchTreeNode<T> *prev_node = 0; // 头节点
BinarySearchTreeNode<T> *node = root;
// 找到值的节点
while (node)
{
// 如果node的值等于data
if(node->data == data)
{
break;
}
prev_node = node; // node的头节点
// node 的值大于deta 就往左子树找
if(node->data > data)
{
node = node->left;
}
// node 的值小于 data 就往右子树找
else{
node = node->right;
}
}
// 找到值的节点了
if(node != 0 && node->data == data)
{
// 如果是头节点
if(node == root)
{
// deleteNodeByMerge(root);
deleteNodeByCopy(root);
}
// 其他节点的左节点==data
else if(prev_node->left == node)
{
// deleteNodeByMerge(prev_node->left);
deleteNodeByCopy(prev_node->left);
}
else
{
// deleteNodeByMerge(prev_node->right);
deleteNodeByCopy(prev_node->right);
}
treeNodeNum--; //节点数减一
return true;
}
else
{
cout << data << "no exits tree" << endl;
}
return false;
}
// 复制删除
template<class T>
bool BinarySearchTree<T> ::removeNodeCopy(const T data)
{
if(isEmpty())
{
cout << "the tree is empty" << endl;
return false;
}
BinarySearchTreeNode<T> *node = root;
BinarySearchTreeNode<T> *prev = 0;
// 找到数据的节点
while (node)
{
// 找到值就跳出循环
if(node->data == data)
{
break;
}
// 未找到,父节点给prev
prev = node;
// data > value -> 右子树查找
if(data > node->data)
{
node = node->right;
}
// 左子树查找
else
{
node = node->left;
}
}
// 找到节点
if(node && node->data == data)
{
// 节点为根节点
if(node == root)
{
deleteNodeByCopy(root);
}
// 右节点
else if(prev->right == node)
{
deleteNodeByCopy(prev->right);
}
// 左节点
else
{
deleteNodeByCopy(prev->left);
}
// 节点数-1
treeNodeNum--;
return true;
}
// 未找到
else
{
cout << data << "no exits in zhe tree" << endl;
}
return false;
}
数据的查询
template<class T>
void BinarySearchTree<T> ::DLR(BinarySearchTreeNode<T> *node)
{
if(!node)
{
return;
}
// 前序遍历(DLR)(根->左->右)
cout << node->data << "->";
DLR(node->left);
DLR(node->right);
}
template<class T>
void BinarySearchTree<T> ::LDR(BinarySearchTreeNode<T> *node)
{
if(!node)
{
return;
}
// 中序遍历(LDR)(左->根->右)
LDR(node->left);
cout << node->data << "->";
LDR(node->right);
}
template<class T>
void BinarySearchTree<T> ::LRD(BinarySearchTreeNode<T> *node)
{
if(!node)
{
return;
}
// 后序遍历(LRD)(左->右->根)
LRD(node->left);
LRD(node->right);
cout << node->data << "->";
}
template<class T>
void BinarySearchTree<T> ::showNodeByDLR()
{
if(isEmpty())
{
cout << "this tree is empty" << endl;
return;
}
// 遍历树
BinarySearchTreeNode<T> *node = root;
cout << "DLR: ";
DLR(node);
cout << endl;
}
template<class T>
void BinarySearchTree<T> ::showNodeByLDR()
{
if(isEmpty())
{
cout << "this tree is empty" << endl;
return;
}
// 遍历树
BinarySearchTreeNode<T> *node = root;
cout << "LDR: ";
LDR(node);
cout << endl;
}
template<class T>
void BinarySearchTree<T> ::showNodeByLRD()
{
if(isEmpty())
{
cout << "this tree is empty" << endl;
return;
}
// 遍历树
BinarySearchTreeNode<T> *node = root;
cout << "LRD: ";
LRD(node);
cout << endl;
}
template<class T>
bool BinarySearchTree<T> ::SearchData(const T data)
{
if(isEmpty())
{
return false;
}
BinarySearchTreeNode<T> *node = root;
while (node)
{
if(node->data == data)
{
return true;
}
else if(data > node->data)
{
node = node->right;
}
else
{
node = node->left;
}
}
return false
;
}
测试
int main(int argc, char const *argv[])
{
BinarySearchTree<int> tree;
tree.inseartNode(5);
tree.inseartNode(3);
tree.inseartNode(2);
tree.inseartNode(4);
tree.inseartNode(6);
tree.inseartNode(5);
tree.inseartNode(7);
// 前序遍历
tree.showNodeByDLR();
// 中序遍历
tree.showNodeByLDR();
// 后序遍历
tree.showNodeByLRD();
cout << "*******************************" << endl;
cout << tree.removeNodeMerge(5) << endl;
// 前序遍历
tree.showNodeByDLR();
// 中序遍历
tree.showNodeByLDR();
// 后序遍历5
tree.showNodeByLRD();
cout << "nodes is:" << tree.Nodes() << endl;
cout << "*******************************" << endl;
cout << tree.removeNodeCopy(7) << endl;
// 前序遍历
tree.showNodeByDLR();
// 中序遍历
tree.showNodeByLDR();
// 后序遍历
tree.showNodeByLRD();
cout << "nodes is:" << tree.Nodes() << endl;
cout << "*******************************" << endl;
cout << tree.SearchData(21) << endl;
system("pause");
return 0;
}
源码